Transforming pseudo-triangulations
Pseudo-Triangulation.
Pseudo-triangle is a simple polygon with exactly three convex
vertices.
Pseudo-triangulation of n points is a partition
of their convex hull into interior disjoint pseudo-triangles whose
vertices are given points.
Minimum pseudo-triangulation of S is a
pseudo-triangulation with the least number of edges among all
pseudo-triangulations of S.
 |
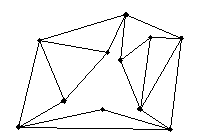 |
| Fig. 1. Pseudo-triangle. | Fig. 2. Minimum pseudo-triangulation of 11 points. |
The basic operation on pseudo-triangulations is a flip.

Fig. 3. (a) Flip of traingles, (b) flip of pseudo-triangles.
Flip Distance. Let T1 and T2 be two trangulations of the same set of points. Flip distance is the minimum number of flips to transform T1 to T2.

Fig. 4. Flip distance between two triangulations is 4.
Flip distance between two pseudo-triangulations is defined in the same way.

Fig. 5. Flip distance between two pseudo-triangulations is 2.
We study the problem of transforming pseudo-triangulations in the plane. We show that a pseudo-triangulation with n vertices can be transformed into another one using O(nlogn) flips only. This improves the previous bound O(n2) of Brönnimann et al. [Fall Workshop on Comput. Geometry, 2001]. We present an algorithm for computing a transformation between two pseudo-triangulations in O((f+n)logn) time where f is the number of flips.
Keywords: Pseudo-triangles; Pseudo-triangulations; Flips; Analysis of algorithms; Computational geometry; Triangulation of a polygon.
@article{b-tpt-04,
author = {Sergey Bereg},
title = {Transforming Pseudo-Triangulations},
journal = {Information Processing Letters},
year = {2004},
volume = {90},
number = {3},
pages = {141--145},
url = {http://dx.doi.org/10.1016/j.ipl.2004.01.021}
}