 Quantum Transport Theory of Resonant-Tunneling Diodes
Quantum Transport Theory of Resonant-Tunneling Diodes  Quantum Transport Theory of Resonant-Tunneling Diodes
Quantum Transport Theory of Resonant-Tunneling Diodes In the early 1980's Bob Bate analyzed the trends of the semiconductor industry and concluded that new device concepts based upon quantum effects would be required to keep the exponential growth trends going into the 21st century. At about this time, Gerry Sollner and co-workers at MIT-Lincoln Lab reported the first quantum-well resonant-tunneling diode (RTD) with respectable performance. The RTD was quickly adopted at TI and elsewhere as the prototypical quantum semiconductor device.
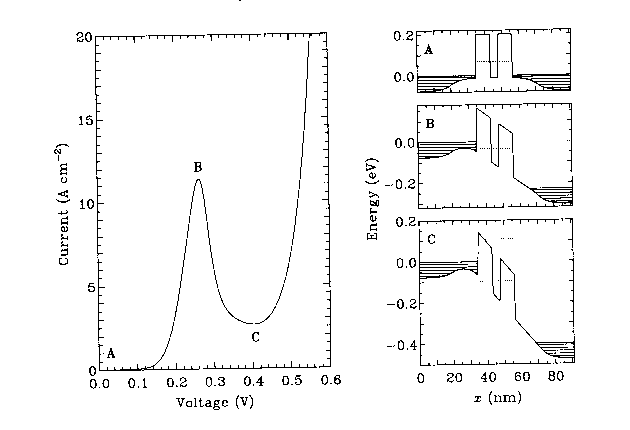
I joined the Nanoelectronics program in mid 1984, and began to address the problem of theoretically modeling devices such as the RTD. The objective was to produce a thorough numerical simulation tool, which would address both the steady-state and transient behavior of the device. This excluded most of the traditional techniques of theoretical physics for dealing with tunneling systems.
The first problem was to define an appropriate representation for the state of the device. This had to represent the ensemble of electrons in the device, and accomodate both the notions of quantum coherence and incorherent superposition. The obvious object to do this was the (von Neumann) density matrix, and based upon experience in device simulation, it was obvious that it should be represented on a real-space basis.
The fundamental approach was to start with an equilibrium density matrix obtained by integrating the Bloch equation with respect to inverse temperature. Then a bias would be applied to the device, and the Liouville-von Neumann equation would be integrated to obtain the transient response. There were two things which had to be added to the ordinary quantum theory to simulate an electron device. One was some notion of dissipation, or random scattering. I found several idealized and/or ad hoc models of such processes. The other problem was that of Ohmic contact boundary conditions. One does not have a device simulation if there is no current flow into and out of the device. An apparently elegant solution was to set the gradient along the diagonal direction of the density matrix equal to zero at the boundaries. This essentially matched up the domain to a spatially uniform semi-infinite reservoir region.
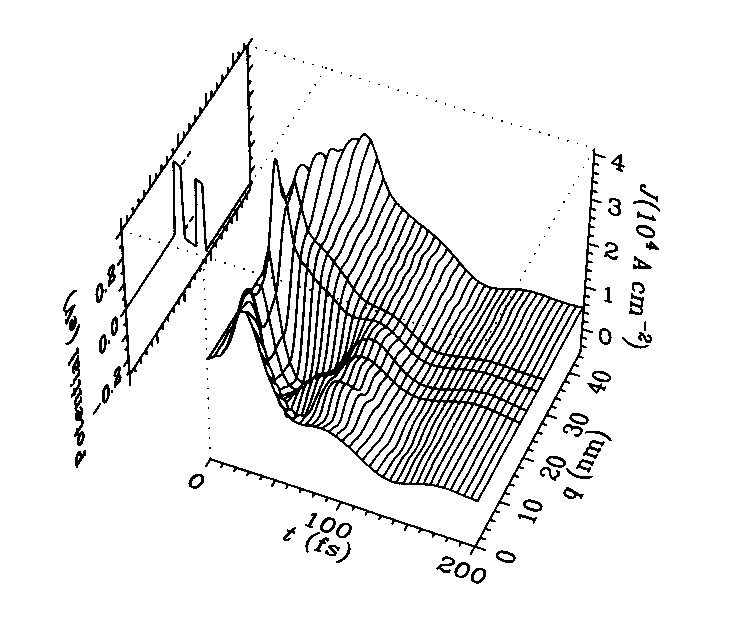
After a number of problems with the mathematical implementation of these schemes, I started a full-up simulation run in late October 1985. The calculations were performed on a VAX-750 system, and consequently took several days of CPU time over a period of more than a week. The results are shown below. (I appologize for the quality. These are scans of some old and faded HP plotter outputs.) The plot is an isometric projection of the lower triangle of the density matrix. The plot on the "horizon" represents the elecron density distribution.
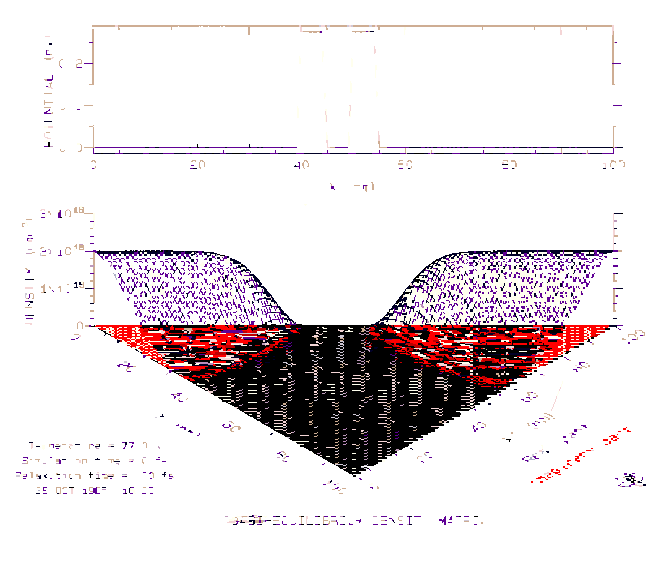
This is the initial, equilibrium state of the device.
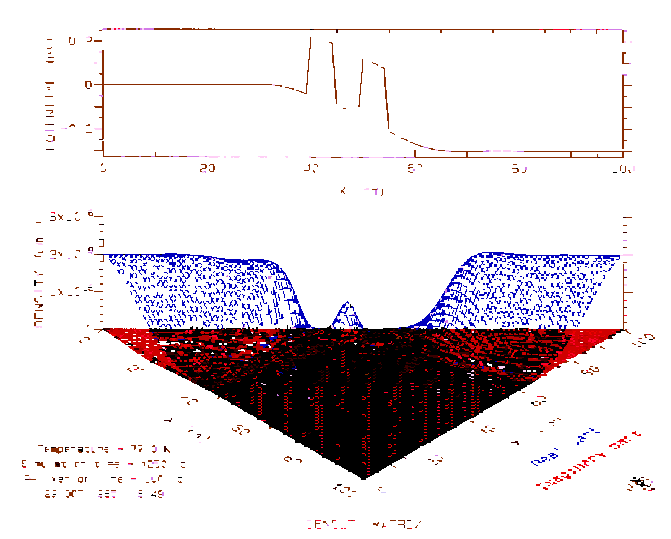
The voltage bias has been applied, and the time evolution algorithm run for a few hundred femtoseconds, and the small peak of electron density building up in the quantum well indicates that tunneling is occuring. A very encouraging result.

After something more than a picosecond of simulated elapsed time, things are begining to look a bit more problematic. The density should not have built up so high, as the electric fields ought to be draining electrons from the quantum well.

After a rather long simulated time, there is definitely a problem here. The unstable growth of the quantum well charge density is clearly unphysical.
After a good deal of casting about, I tracked down the source of the trouble. It was the effect of the Ohmic contact (or open system) boundary conditions on the eigenvalue spectrum of the Liouville-von Neumann superoperator. I had not been too concerned with superoperator algebra before, but what I was implementing in code turned out to be a non-Hermitian superoperator. Here's the story:
If you set up the Liouville operator for a closed system with no dissipation, its eigenvalue spectrum looks like (a) below, the eigenvalues are all purely real. If we add a dissipation superoperator the the Liouville operator, as one expects, the eigenvalues now acquire a negative imaginary part, which turns into a decaying exponential when inserted into the Liouville equation. There is one zero eigenvalue, which represents the equilibrium state of the system.

Now, however, if we modify the boundary conditions to open the system, we break the Hermiticity of the Liouville operator. But the boundary conditions that do so are time-reversible, so we introduce imaginary parts to the eigenvalues, but they occur in conjugate pairs, so there is a growing exponential solution for every decaying exponential [(a) below]. If we add in dissipation, the growing solutions are somewhat damped, but not completely (b). This explains what happened in the RTD simulations. Increasing the dissipation rate can result in a stable solution, but in doing so, one essentially kills all of the coherent effects (c).

I finally realized that the problem is that one can't apply open-system boundary conditions which are also time-reversible. Or, to put it another way, if you open the system, you have to do so in a way that breaks the time-reversal symmetry. This can be done if we transform the density matrix into the Wigner distribution function, and apply different boundary conditions to inflowing and outflowing particles. Such a formulation solves the stability problem, as illustrated by the eigenvalue distribution below.

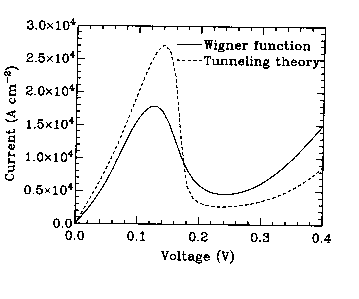
I also demonstrated a realistic calculation of the (intrinsic) transient response of the RTD:
And, finally, small-signal ac response calculations to linear and nonlinear orders:

