Mathematical Properties

Having demonstrated the computational utility of the time-irreversible open-system model defined by (4.33) and (4.36), let us examine its properties in more detail. First, note that the Wigner function derived from a steady-state (4.56) or transient solution of (4.33) is purely real-valued, because both the Liouville equation (4.33) and the boundary conditions (4.36) are purely real. This implies that the corresponding density matrix is Hermitian, as required.

Figure 20. Domain of the density matrix and the Wigner distribution function. The arguments of the density matrix are x and . The Wigner function is obtained by transforming to the coordinates q and r, followed by a Fourier transform with respect to r. The long-dashed lines indicate the system-reservoir boundaries, and they partition the domain into regions corresponding to the various system-system, system-reservoir and reservoir-reservoir correlations. The short-dashed lines represent the boundaries of the domain of the Wigner-distribution-function model. Note that the Wigner function includes contributions from regions which represent correlations with the reservoirs.

Now consider the domain upon which the model is defined, as contrasted to the domain of a spatially closed system. This is illustrated in Fig. 20. For a closed system of length l (bounded by an infinite potential well) the state of the system would be described by a density matrix defined within the square formed by the long-dashed lines. The coordinate rotation from the Wigner-Weyl transformation (4.30) implies that the domain of the Wigner function maps onto the rotated square (``diamond-shaped domain'') shown by the short-dashed lines in the x, 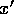plane. The density operator is, in effect, a spatial correlation function. The partitioning of a one-dimensional ``universe'' into a finite system bounded by two semi-infinite reservoirs partitions the domain of the density operator into regions corresponding to various system-system, system-reservoir, and reservoir-reservoir correlations. The domain of the Wigner function does not coincide with that of the system-system density operator, and the Wigner function domain extends into regions which describe system-reservoir correlations. This may well be a necessary characteristic of any useful open-system model.

It must be admitted that the shape of the Wigner function domain as shown in Fig. 20 introduces certain mathematical difficulties. These arise when one requires the density operator given the Wigner function and vice versa. First let us note that the Wigner-Weyl transformation of the density operator into the Wigner function is a unitary superoperator in the sense of (2.6) if the domain [in 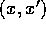and ] is unbounded. This follows from the equivalence of the inner products (2.4) and (4.52). If the domains in and are bounded and do not coincide, the Wigner-Weyl transformation cannot be unitary (and is in fact noninvertible), because some of the information contained in either the Wigner function or the density operator will be lost. This is precisely the situation illustrated in Fig. 20. An additional problem arises in the discrete model which involves the form of the discrete mesh in the two coordinate systems. This is illustrated in Fig. 21, which shows a discrete mesh in and superimposed upon it the rectangular mesh in employed in (4.42). In addition to the loss of information from the corner triangles described above, there is also a loss of information because the 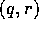meshpoints are only half as dense as the meshpoints. The relation between these two meshes can be summarized as 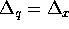and 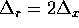. [This mesh is implicitly used in (4.43).] If the 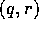mesh were set up with 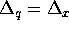and 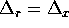, half of the 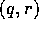mesh points would not coincide with the points. 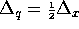A way to incorporate all the points might be to use a staggered mesh in with and 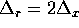. Mains and Haddad (1989) have investigated such a scheme.

Figure 21. Illustration of the inconsistency between discretizations for the density operator and the Wigner function. The squares represent the elements of a bounded, discrete density operator. To transform this into a Wigner function only the filled squares may be employed because they form a discrete, rectangular mesh in the space. This leaves not only the elements in the corner triangles of the density operator unused, but only one-half of the remaining elements are employed. As a result, the transformation from discrete density operator to discrete Wigner function is not unitary.

In summary, one cannot rigorously derive a Wigner function from a density operator and vice versa on a finite, and particularly on a discrete, domain. As a result, any discussions which rely upon the equivalence between the Wigner function and the density operator in such a case must be regarded as plausibility arguments rather than derivations. A more practical consequence is that we have no adequate way to evaluate the operator properties, such as the eigenvalue spectrum or the inverse, of a Wigner function defined upon a bounded domain.

The shape of the natural domain for the Wigner function is a consequence of its relationship with the superoperators generated by x and 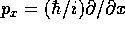. In terms of the variables q, p, and r, these superoperators have particularly simple forms:

The Wigner function is thus expressed in terms of the eigenvalues of and 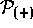, and the fact that these superoperators commute (2.13) is what allows us to define the Wigner function in the first place (because its arguments are the eigenvalues of these superoperators). This observation is the point from which to begin to address one of the obvious concerns connected with any phase-space formulation of a quantum problem: the possibility of a violation of the uncertainty principle. Because q and p are eigenvalues of commuting superoperators, specifying boundary values localized in the plane does not necessarily lead to a violation of the uncertainty principle.

How, then, does the uncertainty principle affect the Wigner function? The usual characteristic of a distribution function which violates the uncertainty principle is that it contains some states which have negative occupation probabilities. That is, the corresponding density matrix will have at least some negative eigenvalues. Consider, for example, a distribution function 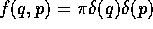, which clearly violates the uncertainty principle. The corresponding density matrix is 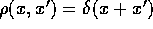. If we operate on any antisymmetric state 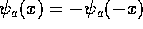with this density matrix, we get 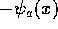, so -1 is certainly an eigenvalue of , which is thus not a valid density matrix. [Note, however, that examples of distribution functions which satisfy the uncertainty principle and are still not valid Wigner functions have been found (Narcowich and O'Connell, 1986).]

Therefore, to represent an acceptable mixed state, the density operator 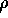must be a positive operator. (Recall that we have modified the normalization condition so that 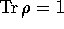is no longer a requirement.) The positivity of 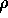and thus of f as an operator does not imply that 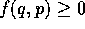. It is well known that the Wigner function can take negative values (Wigner, 1971), and that such negative values are related to quantum interference, as we have seen. One can test the positivity of 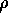using two different conditions (Narcowich and O'Connell, 1986). The most commonly invoked approach is to demand that

for all states . The expectation value can be rewritten as an operator inner product (2.4) by defining the projection operator :

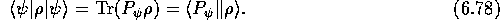
Then the condition (6.77) can be transformed into the Wigner-Weyl representation using (4.52) to obtain the condition

(where 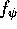is the Wigner function for the pure state 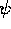) for all 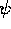. The application of this condition to the distribution functions obtained from the open-system model is hindered by the problems of incompatibility of the finite domains discussed above. In the second test for positivity of the density operator one demands that it should be possible to factor into

where A is some operator (Narcowich and O'Connell, 1986). Applying this condition to the corresponding distribution function requires the expression for the operator product in terms of Wigner functions (Hillery, O'Connell, Scully and Wigner, 1984). Condition (6.80) then becomes (Narcowich and O'Connell, 1986)

where is the Wigner-Weyl transform of A. It appears that the obvious ways to restrict the limits of integration in (6.81) to a finite domain lead to expressions which violate at least one of the semi-group axioms which define operator multiplication. If an expression which does satisfy those axioms could be derived from (6.81), we would obtain a useful definition of positivity in the open-system case.

Now, does the procedure of directly solving for the Wigner function under inhomogeneous boundary conditions lead to a positive 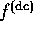operator? In the absence of a rigorous definition of positivity for a Wigner function on a finite domain, there is, of course, no mathematical demonstration which guarantees such positivity. It may well be possible to define a case of the present open-system model which does violate the uncertainty principle. However, let us qualitatively explore some of the considerations which bear upon this question. First, note that the positivity of necessarily involves the positivity of the boundary values, because is a linear function of the boundary values as shown by (4.56). We can speculate that at least in a semiclassical situation should be a positive operator if and are positive. To establish the plausibility of the idea, let us consider the classical case. The properties of the classical Liouville equation (4.35) employing the open system boundary conditions (4.36) are essentially the same as those of the quantum case with respect to the eigenvalue spectrum of the Liouville operator and the stability of the resulting solutions. If we assume that there is no damping within the system, then the classical Liouville theorem holds within the system, and the distribution function is constant along the classical trajectories (which are the characteristic curves of the Liouville equation). Any trajectory passing through a boundary must in fact pass through a boundary twice, once as an incoming particle and once as an outgoing particle (otherwise a density would have to build up in violation of the Liouville theorem). Such trajectories cover the phase space, except for those regions which correspond to any bound orbits. Because is constant along a trajectory and its value is fixed by the boundary condition, 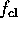must be nonnegative if, and only if, the boundary values are nonnegative. 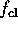The values of in regions corresponding to bound states will be nonnegative if and only if the initial values of 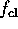(with respect to time) are nonnegative.

How might these considerations be modified in a quantum-mechanical system? Or, in other words, how can one get into trouble applying the open-system boundary conditions to a quantum system? The only obvious case would be an attempt to apply the boundary conditions (4.36) in a region where there were strong interference effects, such as standing waves. We can easily imagine that, for example, forcing f to have a large density at a boundary point where a node in the density should occur would introduce spurious states with negative occupation. To avoid such situations, one should apply (4.36) only in reasonably classical regions of a system. In practice, this means at least a few times the thermal coherence length (3.18) away from any abrupt feature of the potential (where the standing waves are smeared out by thermal incoherence). At lower temperatures, one would use the reciprocal of the Fermi wavevector, rather than .

Now let us examine in more detail the mathematical structure of the model which results from the time-irreversible boundary conditions. The discrete expression for the drift term of the Liouville equation (4.48) has the form of a master operator (Bedeaux, Lakatos-Lindenberg, and Shuler, 1971). Such an operator, when applied to a distribution function, has the effect of removing some fraction of the density in each possible state and redistributing that fraction among the other possible states. For a finite, discrete model the properties of the matrix M representing a master operator are:

In the last condition the column sum is actually equal to zero except for those states j which can lose density to an external reservoir, as is the case for the open system model on the outflowing boundaries. All the eigenvalues of a matrix satisfying the conditions (6.82) will have nonpositive real parts (Oppenheim, Shuler, and Weiss, 1977, ch. 3). This may be readily demonstrated by appealing to Gerschgorin's theorem (Wilkinson, 1965), which states that every eigenvalue of a matrix A lies in at least one of the circular discs (in the complex plane) with centers at 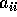and radii 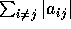. To apply this theorem to the master operator M, let us take the matrix A to be the transpose of M, , to change the column sum condition into a row sum. The eigenvalues of M and A are identical. Then because is negative for i=j and positive for 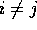and is real for all i and j, we find that the real part of each eigenvalue must satisfy

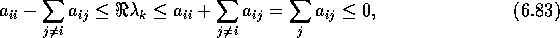
for some i. Thus, 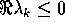for all k. The fact that the column sums in for the outflow boundaries are less than zero makes 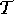nonsingular. (In a master operator describing a closed system, all the column sums would be zero, which implies that the determinant would be zero, so there must be an eigenvalue equal to zero.)

The fact that the upwind discretization generates a master operator is the fundamental reason for its success, both in the present context and in the more traditional applications of transport theory (Roache, 1976, pp 4--5; Duderstadt and Martin, 1979). Now, in the quantum case, the complete Liouville operator (in the Wigner-Weyl representation) cannot be a master operator, because we know that the Wigner distribution can have negative values, which a master operator would not permit. As we have noted, the quantum interference phenomena enter the Wigner distribution via the potential superoperator 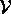. The fundamental result of the present work is the demonstration in Fig. 9 and equations (4.53)-(4.54) that the Markovian model which follows from the irreversible boundary conditions (4.36) introduces the necessary stability properties in the quantum case as well as in the much more obvious classical case.

It is interesting to consider the form assumes upon transformation back to a real-space density matrix representation. For this purpose let us assume that we have defined the Wigner function on a discrete basis with respect to q and on a continuum basis with respect to p. Then 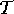is given by

To transform this back to the density matrix representation, we must evaluate

with (4.32) substituted for f. [To simplify the resulting expressions, we will express the arguments of in terms of q and r of equation (4.30) and Fig. 20.] Evaluation of (6.85) requires the formula

and its complex conjugate. Letting 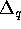approach zero we find

The second term in (6.87) contributes an anti-Hermitian component to 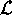. The appearance of in this term is reminiscent of the ``numerical viscosity'' which is a property of some finite-difference formulations of transport equations (Press, Flannery, Teukolsky, and Vetterling, 1986). The principal-value integral in (6.87) has the desired effect of distinguishing the sign of the momentum of the states present in . To see this, suppose that there is a term contained in 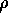. One could evaluate its contribution to the integral in (6.87) by contour integration, closing the contour in the upper or lower half-plane if k were positive or negative, respectively. But then the sign of the contribution of the pole on the real axis changes as the sign of k changes. The anti-Hermitian term vanishes, except possibly for a surface contribution, in the limit .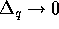

This description of open systems in terms of has not yet been developed into a workable model. However, there is a strong motivation for doing so in the context of semiconductor heterostructures. In such a structure the electron energy-momentum relation can be considerably more complex than a simple parabola, and it changes from one material to another in ways which cannot be represented by a shift in the local potential. The simplest example of such an effect is the change in effective mass as an electron crosses a heterojunction. As described in Appendix 13, this leads to a highly nonlocal form for the kinetic energy superoperator in the Wigner-Weyl representation. More complex features of the energy-band structure can be modeled by any of a number of localized-basis-function schemes which may require more than one basis function per lattice site. 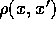Such schemes could easily fit into an approach expressed in terms of , but it is not at all obvious how to incorporate such effects into the Wigner function in view of the incompatible discretization requirements illustrated in Fig. 21.

Of more general interest is the appearance of (6.86) in the deductive chain leading to (6.87). Such a relation, more often expressed in the form

is usually encountered in the analysis of irreversible quantum phenomena. It is the mathematical expression of the fact that a continuum of states (and therefore of frequencies) provides enough degrees of freedom that a Poincaré recurrence can be postponed indefinitely.

It appears in the analysis of behavior in the time and frequency domains, and is used to express the initial conditions which lead to irreversible behavior: no advanced waves in electrodynamics (Bjorken and Drell, 1964), or adiabatic switching-on in many-body theory (Kohn and Luttinger, 1957; Fetter and Walecka, 1971). In the present model such a relation appears in the position and momentum domains and expresses the effects of the spatial boundary conditions.