


Next: Relation to Many-Body
Up: PROPERTIES OF THE
Previous: Mathematical Properties
One of the benefits of the time-irreversible open-system boundary
conditions is that they provide an alternative to the use of periodic
boundary conditions in the analysis of quantum-transport phenomena. The
great disadvantage of periodic boundary conditions is that they do not
address the case in which the potential varies significantly
across a system. That is, their use restricts one to the study of
low-field phenomena. It has been pointed out (Yennie, 1987, footnote 11
acknowledging private discussion with M. Weinstein) that
quasi-periodic boundary conditions ( i.e., periodic within a phase
factor which can be removed by a gauge transformation) are necessary if
the momentum operator is to be Hermitian on a finite domain. The
present work demonstrates that far-from-equilibrium phenomena can be
modeled by employing a non-Hermitian momentum superoperator.
The connection between symmetries and conservation laws is
undoubtedly one of the most fundamental results of the quantum theory.
However, if one is faced with the task of describing the behavior of a
nonconservative system, the inability to modify or violate the
conservation laws becomes an obstacle to defining a realistic model,
rather than a benefit. The problem is that one wants a model whose
solutions stably approach a steady state, which requires complex-valued
eigenvalues, but the expectation values of physical observables should
be real. The present analysis of open-system models demonstrates that
these conflicting requirements can be accommodated at the kinetic level,
because the roles of generating the dynamical evolution and evaluating
observables are filled by different superoperators. If we
reexamine the models described above, we find that the dynamic effects
such as generating time evolution or moving density by current flow are
described by commutator superoperators, and these are the superoperators
which become non-Hermitian when one incorporates interactions with the
outside world. The measurement of the expectation values of observables
is done by anticommutator superoperators, and these, with proper
attention to the definition of the domain and boundary conditions, remain
Hermitian. This separation of function has been noted by Prigogine
(1980) in the superoperators generated by the Hamiltonian.
In the open-system model the momentum superoperators appear in similar
roles, and this demonstrates the existence of a more general underlying
structure in the kinetic theory.
Let us consider the superoperators  and
and  derived from the momentum operator. We have already observed that the
kinetic energy term of the Liouville equation (2.3) can be
written as
derived from the momentum operator. We have already observed that the
kinetic energy term of the Liouville equation (2.3) can be
written as  (3.21).
(3.21).
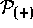 will be Hermitian if we restrict our
attention to density matrices whose off-diagonal elements approach zero
for large
will be Hermitian if we restrict our
attention to density matrices whose off-diagonal elements approach zero
for large 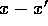 (so that integration by parts may performed
without a surface contribution in an integral over
(so that integration by parts may performed
without a surface contribution in an integral over  ).
Such density matrices describe normal systems
(as opposed to superconducting, or with some other long-range coherent
effect) at nonzero temperature. In such normal cases
).
Such density matrices describe normal systems
(as opposed to superconducting, or with some other long-range coherent
effect) at nonzero temperature. In such normal cases 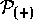 produces the real-valued factor p in the drift term (4.38).
produces the real-valued factor p in the drift term (4.38).
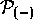 generates the gradient in
generates the gradient in  and is thus the
superoperator which is rendered non-Hermitian by the boundary conditions
(4.36).
and is thus the
superoperator which is rendered non-Hermitian by the boundary conditions
(4.36).
We can also see the dichotomy of function between 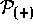 and
and
 by examining the elementary quantum continuity equation,
which is conventionally written
by examining the elementary quantum continuity equation,
which is conventionally written

where

By now we should readily recognize the presence of 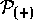 in the
current density operator J. In fact, the current density is much more
naturally regarded as a superoperator,
in the
current density operator J. In fact, the current density is much more
naturally regarded as a superoperator,

and we see  in the role of measuring an observable. At the
kinetic level the continuity equation is linear in terms of the density
matrix
in the role of measuring an observable. At the
kinetic level the continuity equation is linear in terms of the density
matrix 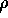 and is simply the Liouville equation evaluated along the
diagonal
and is simply the Liouville equation evaluated along the
diagonal  .
.
The continuity equation is of course just the zeroth-order moment equation
of the Liouville equation. The higher-order moments of the Liouville
equation may be obtained by operating on the equation with 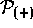 (or
(or  ) and evaluating the resulting expression along the
diagonal. Let
us denote the evaluation of an operator kernel for
) and evaluating the resulting expression along the
diagonal. Let
us denote the evaluation of an operator kernel for  by
angle brackets,
by
angle brackets,  .
This is equivalent to the phase-space procedure of
multiplying by some power of p and then integrating over all p, so
that the corresponding expression for the Wigner function is
.
This is equivalent to the phase-space procedure of
multiplying by some power of p and then integrating over all p, so
that the corresponding expression for the Wigner function is
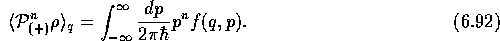
The moment
equations we will derive are a special case of those which have been
discussed by a number of authors (Frölich, 1967; Putterman, 1974;
Iafrate, Grubin, and Ferry, 1981; Kreuzer, 1981),
because we will not consider two-body or dissipative interactions.
The objective is to
demonstrate the role of the anticommutator superoperators in this
procedure, a point which has not been previously articulated.
As a starting point
from which to derive the moment equations, let us rewrite the Liouville
equation in superoperator notation, making use of the factorization
(3.21):

The manipulations required to generate the moment equations may be
considerably simplified by using some superoperator relations to
evaluate the effect of  on the potential and its
derivatives. To derive the necessary expressions, let us consider an
operator
on the potential and its
derivatives. To derive the necessary expressions, let us consider an
operator  , which is diagonal in position
space. The commutators of the derived superoperators
, which is diagonal in position
space. The commutators of the derived superoperators 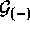 and
and
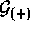 with
with 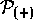 are then
are then
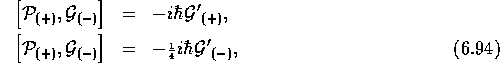
where  indicates the superoperator derived from the spatial
derivative
indicates the superoperator derived from the spatial
derivative  . Note that
. Note that
 for any such operator, and
for any such operator, and
 for
any operator
for
any operator  . Now we may readily derive the moment equations.
The zeroth moment is thus
. Now we may readily derive the moment equations.
The zeroth moment is thus

which is a familiar form of the continuity equation. If a collision
term is included in the kinetic equation, it must have a form such that
 if the theory is to satisfy the
continuity equation. This means that
if the theory is to satisfy the
continuity equation. This means that  in
the density matrix representation [a condition satisfied by the
Fokker-Planck operator (3.23)]
or
in
the density matrix representation [a condition satisfied by the
Fokker-Planck operator (3.23)]
or  with
with  ,
for the Wigner function (see Appendix 14).
,
for the Wigner function (see Appendix 14).
The first moment equation is readily found to be

where  is the momentum flux density. [For
two- or three-dimensional models, the direct product of the two vectors
is the momentum flux density. [For
two- or three-dimensional models, the direct product of the two vectors
 is taken and
is taken and  will be a tensor
(Landau and Lifshitz, 1959).] Equation (6.96)
is identical to its classical counterpart. If we
integrate it with respect to q (assuming that the domain is
rectangular in the
will be a tensor
(Landau and Lifshitz, 1959).] Equation (6.96)
is identical to its classical counterpart. If we
integrate it with respect to q (assuming that the domain is
rectangular in the  coordinates and extends over
0 < q < l), we obtain a generalization of Ehrenfest's theorem
to the case of an open system:
coordinates and extends over
0 < q < l), we obtain a generalization of Ehrenfest's theorem
to the case of an open system:
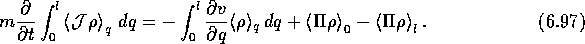
The last two terms represent the effect of opening the system: a flux
of momentum density through the boundaries of the system will affect the
current flow within the system. To make contact with hydrodynamics, we
would follow the standard kinetic-theory manipulations (Kreuzer, 1981,
ch. 8)
and define a kinetic pressure tensor  and separate
and separate  into
into
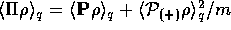 .
.
Continuing with the above procedure, we may derive a second-moment
equation by operating on (6.93) with  to
obtain
to
obtain

Quantum corrections in the form of terms containing  will begin to appear in the third and higher moment
equations, as one would expect from the Wigner-Moyal expansion
(4.41). However, the second moment equation presents something
of an ambiguity. We might also derive it by operating on
(6.93) with the
will begin to appear in the third and higher moment
equations, as one would expect from the Wigner-Moyal expansion
(4.41). However, the second moment equation presents something
of an ambiguity. We might also derive it by operating on
(6.93) with the  derived from the kinetic energy operator T. These are not at all the
same superoperators:
derived from the kinetic energy operator T. These are not at all the
same superoperators:

Putterman (1974) displays both of these forms and notes that
both lead to the same bulk properties, thus any physical difference must
appear in a surface contribution. It is not the purpose of the present
discussion to investigate these issues in detail, but only to
demonstrate that anticommutator superoperators appear naturally in any
attempt to evaluate expectation values in kinetic theory.
The same dichotomy between commutator and anticommutator
superoperators can be seen in the case of the superoperators generated
by the Hamiltonian H. Of course  is just the Liouville
superoperator
is just the Liouville
superoperator  , and we have examined at length the need for a
departure from Hermiticity in the case of
, and we have examined at length the need for a
departure from Hermiticity in the case of 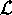 . We have not yet
encountered a need for the anticommutator
. We have not yet
encountered a need for the anticommutator  . One place
it does occur is in a generalization of the Bloch equation
(3.16) to the case of an open system. If one attempts to
compute an equilibrium density matrix as a finite segment of a much
larger system by modifying the boundary conditions on
. One place
it does occur is in a generalization of the Bloch equation
(3.16) to the case of an open system. If one attempts to
compute an equilibrium density matrix as a finite segment of a much
larger system by modifying the boundary conditions on 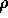 in the
Bloch equation, one quickly discovers that product
in the
Bloch equation, one quickly discovers that product  must be
symmetrized to obtain sensible answers. Thus, the Bloch equation becomes
must be
symmetrized to obtain sensible answers. Thus, the Bloch equation becomes
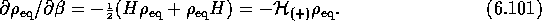
If the time-reversible open-system boundary conditions (3.19)
are applied to the Bloch equation, one obtains a quite useful method for
evaluating the equilibrium density matrix (in contrast to the
disastrous effect these boundary conditions have upon the time
evolution). Taking into account our particle-density normalization of
 , the correct Bloch equation is
, the correct Bloch equation is

with the initial condition

When this equation is integrated, the resulting densities in regions of
constant potential are found to be equal to the semiclassically expected
value  . An example of
an equilibrium density matrix obtained from such a calculation is
illustrated in Fig. 22.
. An example of
an equilibrium density matrix obtained from such a calculation is
illustrated in Fig. 22.

Figure 22.
Equilibrium density matrix obtained by numerically integrating the
generalized Bloch equation (6.102) subject to the reversible
open-system boundary conditions (3.19). The potential,
displayed above, represents the sort of features which are now
realizable using semiconductor heterostructure technology. The chemical
potential  is indicated by the dashed line. The calculation
employed parameters appropriate for the Al
is indicated by the dashed line. The calculation
employed parameters appropriate for the Al Ga
Ga As system at 77
K. The three energy barriers create two identical ``quantum wells,''
bounded by contacting layers. The lowest energy states in these wells
are pushed toward higher energy by size quantization, which reduces the
electron density in the wells via the Boltzmann factor. The shallow
peaks off the diagonal measure the correlation between the phase of the
electron
at different positions, and indicate in the present case that the
symmetric combination of the well states has a greater occupation factor
than the antisymmetric combination.
As system at 77
K. The three energy barriers create two identical ``quantum wells,''
bounded by contacting layers. The lowest energy states in these wells
are pushed toward higher energy by size quantization, which reduces the
electron density in the wells via the Boltzmann factor. The shallow
peaks off the diagonal measure the correlation between the phase of the
electron
at different positions, and indicate in the present case that the
symmetric combination of the well states has a greater occupation factor
than the antisymmetric combination.
Here we see that again the anticommutator superoperator appears in
the role of evaluating an observable, in this case for the purpose of
evaluating the energy and thus the occupation probability of the
possible states. We would expect that, for this purpose, 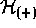 ought to be Hermitian. Its Hermiticity in fact depends upon the shape
of the domain when the boundary conditions (3.19) are applied.
Because
ought to be Hermitian. Its Hermiticity in fact depends upon the shape
of the domain when the boundary conditions (3.19) are applied.
Because  is an elliptic operator, it is easy to show that it
will be Hermitian when the domain is rectangular in the
is an elliptic operator, it is easy to show that it
will be Hermitian when the domain is rectangular in the  coordinates, so that the gradient in (3.19) is normal to the
system boundary. It is not Hermitian when applied to a domain which is
square in the
coordinates, so that the gradient in (3.19) is normal to the
system boundary. It is not Hermitian when applied to a domain which is
square in the  coordinates, as in the calculation
illustrated in Fig. 22. However, the departure from
Hermiticity is small, and the results are physically quite reasonable.
I have not yet implemented a program to perform such a calculation on a
rectangular domain in
coordinates, as in the calculation
illustrated in Fig. 22. However, the departure from
Hermiticity is small, and the results are physically quite reasonable.
I have not yet implemented a program to perform such a calculation on a
rectangular domain in  , but this would be the proper way to
proceed to evaluate the equilibrium density matrix using open-system
boundary conditions.
, but this would be the proper way to
proceed to evaluate the equilibrium density matrix using open-system
boundary conditions.
Having noted that 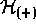 appears in the evaluation of the
equilibrium density matrix, we can address a point raised by Dahl
(1981). It is that
appears in the evaluation of the
equilibrium density matrix, we can address a point raised by Dahl
(1981). It is that  , by itself, does not
define a unique eigenvalue problem in the wavefunction space of
a quantum system; but together
with
, by itself, does not
define a unique eigenvalue problem in the wavefunction space of
a quantum system; but together
with  , it does define such a problem. This consideration
enters the present problem only for bound states localized within the
open system (Carruthers and Zachariasen, 1983).
As noted earlier, such states would lead
to a nontrivial null space of
, it does define such a problem. This consideration
enters the present problem only for bound states localized within the
open system (Carruthers and Zachariasen, 1983).
As noted earlier, such states would lead
to a nontrivial null space of  . The occupation of such states
would have to be determined as an initial condition, such as an
equilibrium distribution evaluated using
. The occupation of such states
would have to be determined as an initial condition, such as an
equilibrium distribution evaluated using  .
.



Next: Relation to Many-Body
Up: PROPERTIES OF THE
Previous: Mathematical Properties
William R. Frensley
Thu Jun 8 17:53:37 CDT 1995
 and
and  derived from the momentum operator. We have already observed that the
kinetic energy term of the Liouville equation (2.3) can be
written as
derived from the momentum operator. We have already observed that the
kinetic energy term of the Liouville equation (2.3) can be
written as  (3.21).
(3.21).
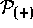 will be Hermitian if we restrict our
attention to density matrices whose off-diagonal elements approach zero
for large
will be Hermitian if we restrict our
attention to density matrices whose off-diagonal elements approach zero
for large 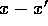 (so that integration by parts may performed
without a surface contribution in an integral over
(so that integration by parts may performed
without a surface contribution in an integral over  ).
Such density matrices describe normal systems
(as opposed to superconducting, or with some other long-range coherent
effect) at nonzero temperature. In such normal cases
).
Such density matrices describe normal systems
(as opposed to superconducting, or with some other long-range coherent
effect) at nonzero temperature. In such normal cases 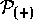 produces the real-valued factor p in the drift term (4.38).
produces the real-valued factor p in the drift term (4.38).
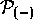 generates the gradient in
generates the gradient in  and is thus the
superoperator which is rendered non-Hermitian by the boundary conditions
(4.36).
and is thus the
superoperator which is rendered non-Hermitian by the boundary conditions
(4.36).
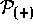 and
and
 by examining the elementary quantum continuity equation,
which is conventionally written
by examining the elementary quantum continuity equation,
which is conventionally written


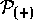 in the
current density operator J. In fact, the current density is much more
naturally regarded as a superoperator,
in the
current density operator J. In fact, the current density is much more
naturally regarded as a superoperator,

 in the role of measuring an observable. At the
kinetic level the continuity equation is linear in terms of the density
matrix
in the role of measuring an observable. At the
kinetic level the continuity equation is linear in terms of the density
matrix 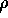 and is simply the Liouville equation evaluated along the
diagonal
and is simply the Liouville equation evaluated along the
diagonal  .
.
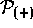 (or
(or  ) and evaluating the resulting expression along the
diagonal. Let
us denote the evaluation of an operator kernel for
) and evaluating the resulting expression along the
diagonal. Let
us denote the evaluation of an operator kernel for  by
angle brackets,
by
angle brackets,  .
This is equivalent to the phase-space procedure of
multiplying by some power of p and then integrating over all p, so
that the corresponding expression for the Wigner function is
.
This is equivalent to the phase-space procedure of
multiplying by some power of p and then integrating over all p, so
that the corresponding expression for the Wigner function is
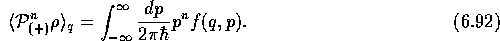

 on the potential and its
derivatives. To derive the necessary expressions, let us consider an
operator
on the potential and its
derivatives. To derive the necessary expressions, let us consider an
operator  , which is diagonal in position
space. The commutators of the derived superoperators
, which is diagonal in position
space. The commutators of the derived superoperators  and
and
 with
with 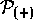 are then
are then
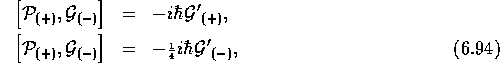
 indicates the superoperator derived from the spatial
derivative
indicates the superoperator derived from the spatial
derivative  . Note that
. Note that
 for any such operator, and
for any such operator, and
 for
any operator
for
any operator  . Now we may readily derive the moment equations.
The zeroth moment is thus
. Now we may readily derive the moment equations.
The zeroth moment is thus

 if the theory is to satisfy the
continuity equation. This means that
if the theory is to satisfy the
continuity equation. This means that  in
the density matrix representation [a condition satisfied by the
Fokker-Planck operator (
in
the density matrix representation [a condition satisfied by the
Fokker-Planck operator ( with
with  ,
for the Wigner function (see Appendix
,
for the Wigner function (see Appendix 
 is the momentum flux density. [For
two- or three-dimensional models, the direct product of the two vectors
is the momentum flux density. [For
two- or three-dimensional models, the direct product of the two vectors
 is taken and
is taken and  will be a tensor
(Landau and Lifshitz, 1959).] Equation (
will be a tensor
(Landau and Lifshitz, 1959).] Equation ( coordinates and extends over
0 < q < l), we obtain a generalization of Ehrenfest's theorem
to the case of an open system:
coordinates and extends over
0 < q < l), we obtain a generalization of Ehrenfest's theorem
to the case of an open system:
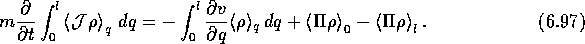
 and separate
and separate  into
into
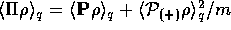 .
.
 to
obtain
to
obtain

 will begin to appear in the third and higher moment
equations, as one would expect from the Wigner-Moyal expansion
(
will begin to appear in the third and higher moment
equations, as one would expect from the Wigner-Moyal expansion
( derived from the kinetic energy operator T. These are not at all the
same superoperators:
derived from the kinetic energy operator T. These are not at all the
same superoperators:

 is just the Liouville
superoperator
is just the Liouville
superoperator  , and we have examined at length the need for a
departure from Hermiticity in the case of
, and we have examined at length the need for a
departure from Hermiticity in the case of 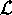 . We have not yet
encountered a need for the anticommutator
. We have not yet
encountered a need for the anticommutator  . One place
it does occur is in a generalization of the Bloch equation
(
. One place
it does occur is in a generalization of the Bloch equation
(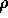 in the
Bloch equation, one quickly discovers that product
in the
Bloch equation, one quickly discovers that product  must be
symmetrized to obtain sensible answers. Thus, the Bloch equation becomes
must be
symmetrized to obtain sensible answers. Thus, the Bloch equation becomes
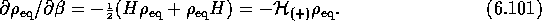
 , the correct Bloch equation is
, the correct Bloch equation is


 . An example of
an equilibrium density matrix obtained from such a calculation is
illustrated in Fig.
. An example of
an equilibrium density matrix obtained from such a calculation is
illustrated in Fig. 
 is indicated by the dashed line. The calculation
employed parameters appropriate for the Al
is indicated by the dashed line. The calculation
employed parameters appropriate for the Al Ga
Ga As system at 77
K. The three energy barriers create two identical ``quantum wells,''
bounded by contacting layers. The lowest energy states in these wells
are pushed toward higher energy by size quantization, which reduces the
electron density in the wells via the Boltzmann factor. The shallow
peaks off the diagonal measure the correlation between the phase of the
electron
at different positions, and indicate in the present case that the
symmetric combination of the well states has a greater occupation factor
than the antisymmetric combination.
As system at 77
K. The three energy barriers create two identical ``quantum wells,''
bounded by contacting layers. The lowest energy states in these wells
are pushed toward higher energy by size quantization, which reduces the
electron density in the wells via the Boltzmann factor. The shallow
peaks off the diagonal measure the correlation between the phase of the
electron
at different positions, and indicate in the present case that the
symmetric combination of the well states has a greater occupation factor
than the antisymmetric combination.
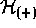 ought to be Hermitian. Its Hermiticity in fact depends upon the shape
of the domain when the boundary conditions (
ought to be Hermitian. Its Hermiticity in fact depends upon the shape
of the domain when the boundary conditions ( is an elliptic operator, it is easy to show that it
will be Hermitian when the domain is rectangular in the
is an elliptic operator, it is easy to show that it
will be Hermitian when the domain is rectangular in the  coordinates, so that the gradient in (
coordinates, so that the gradient in ( coordinates, as in the calculation
illustrated in Fig.
coordinates, as in the calculation
illustrated in Fig. 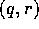 , but this would be the proper way to
proceed to evaluate the equilibrium density matrix using open-system
boundary conditions.
, but this would be the proper way to
proceed to evaluate the equilibrium density matrix using open-system
boundary conditions.
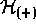 appears in the evaluation of the
equilibrium density matrix, we can address a point raised by Dahl
(1981). It is that
appears in the evaluation of the
equilibrium density matrix, we can address a point raised by Dahl
(1981). It is that  , by itself, does not
define a unique eigenvalue problem in the wavefunction space of
a quantum system; but together
with
, by itself, does not
define a unique eigenvalue problem in the wavefunction space of
a quantum system; but together
with  , it does define such a problem. This consideration
enters the present problem only for bound states localized within the
open system (Carruthers and Zachariasen, 1983).
As noted earlier, such states would lead
to a nontrivial null space of
, it does define such a problem. This consideration
enters the present problem only for bound states localized within the
open system (Carruthers and Zachariasen, 1983).
As noted earlier, such states would lead
to a nontrivial null space of  . The occupation of such states
would have to be determined as an initial condition, such as an
equilibrium distribution evaluated using
. The occupation of such states
would have to be determined as an initial condition, such as an
equilibrium distribution evaluated using  .
.