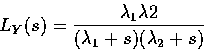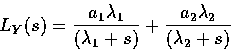The kth moment of a random variable X is given by E[Xk].
The kth central moment of a random variable X is given by
E[(X-E[X])k].
The moment generating function of X is given by:
![\begin{displaymath}M(\theta) = E[e^{X\theta}] = \int_{-\infty}^{\infty} e^{x\theta} f(x) dx.
\end{displaymath}](img5.gif) |
(9) |
If X is non-negative, we can define its Laplace transform:
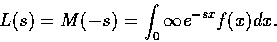 |
(10) |
Taking the power series expansion of
 yields:
yields:
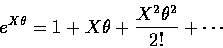 |
(11) |
Taking the expectation yields:
![\begin{displaymath}E[e^{X \theta}] = 1+E[X] \theta + \frac{E[X^{2}] \theta^{2}}{2!} + \cdots
\end{displaymath}](img9.gif) |
(12) |
We can then find the kth moment of X by taking the kth derivative
of the moment generating function and setting  .
.
![\begin{displaymath}E[X^{k}] = \frac{d^{k}M(\theta)}{d\theta^{k}}\left\vert _{\theta=0} \right.
\end{displaymath}](img11.gif) |
(13) |
For the Laplace transform, the moments can be found using:
![\begin{displaymath}E[X^{k}] = (-1)^{k} \frac{d^{k}L(s)}{ds^{k}}\left\vert _{s=0} \right.
\end{displaymath}](img12.gif) |
(14) |
Example:
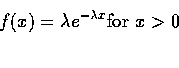 |
(15) |
 |
= |
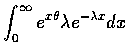 |
(16) |
| |
= |
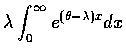 |
(17) |
| |
= |
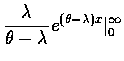 |
(18) |
| |
= |
 |
(19) |
![\begin{displaymath}E[X] = \frac{dM(\theta)}{d\theta}\left\vert _{\theta=0} \righ...
...da}{(\lambda-\theta)^{2}}\vert _{\theta=0} = \frac{1}{\lambda}
\end{displaymath}](img19.gif) |
(20) |
![\begin{displaymath}E[X^{2}] = \frac{d^{2}M(\theta)}{d\theta^{2}}\left\vert _{\th...
...
= \frac{2 \lambda^{2}}{\lambda^{4}} = \frac{2}{\lambda^{2}}
\end{displaymath}](img20.gif) |
(21) |
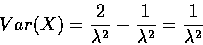 |
(22) |
For X non-negative, integer-valued, and discrete, we can define the
z-transform:
![\begin{displaymath}G(z)=E[z^{X}] = \sum_{i=0}^{\infty} p(i) z^{i}
\end{displaymath}](img22.gif) |
(23) |
The first and second moments can be found as follows:
![\begin{displaymath}E[X]=\frac{dG(z)}{dz}\vert _{z=1}
\end{displaymath}](img23.gif) |
(24) |
![\begin{displaymath}E[X^{2}]=\frac{d^{2}G(z)}{dz^{2}}\vert _{z=1} + \frac{dG(z)}{dz}\vert _{z=1}
\end{displaymath}](img24.gif) |
(25) |
A property of transforms, known as the convolution theorem is
stated as follows:
Let
 be mutually independent random variables.
Let
be mutually independent random variables.
Let
 .
If
.
If
 exists for all i, then
exists for all i, then
 exists, and:
exists, and:
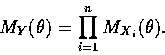 |
(26) |
Example:
Let X1 and X2 be independent exponentially distributed
random variables with parameters
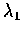 and
and
 respectively. Let
Y = X1+X2. Find the distribution of Y.
respectively. Let
Y = X1+X2. Find the distribution of Y.
The Laplace transforms for X1 and X2 are:
 |
(27) |
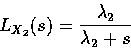 |
(28) |
By the convolution theorem:
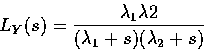 |
(29) |
Expanding this into partial fractions:
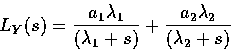 |
(30) |
where:
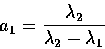 |
(31) |
 |
(32) |
Taking the inverse Laplace transform yields:
 |
(33) |
1999-08-31
![]() yields:
yields:
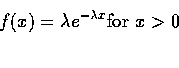
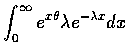
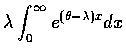
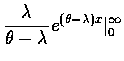

![\begin{displaymath}E[X] = \frac{dM(\theta)}{d\theta}\left\vert _{\theta=0} \righ...
...da}{(\lambda-\theta)^{2}}\vert _{\theta=0} = \frac{1}{\lambda}
\end{displaymath}](img19.gif)
![\begin{displaymath}E[X^{2}] = \frac{d^{2}M(\theta)}{d\theta^{2}}\left\vert _{\th...
...
= \frac{2 \lambda^{2}}{\lambda^{4}} = \frac{2}{\lambda^{2}}
\end{displaymath}](img20.gif)
![\begin{displaymath}G(z)=E[z^{X}] = \sum_{i=0}^{\infty} p(i) z^{i}
\end{displaymath}](img22.gif)
![]() be mutually independent random variables.
Let
be mutually independent random variables.
Let
![]() .
If
.
If
![]() exists for all i, then
exists for all i, then
![]() exists, and:
exists, and:
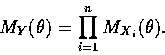
![]() and
and
![]() respectively. Let
Y = X1+X2. Find the distribution of Y.
respectively. Let
Y = X1+X2. Find the distribution of Y.